How and why do technologies spread when and where they do? What are the implications and consequences for the structure, wealth, and management of human organizations? Social and industrial evolutionary processes follow a sequence of replacements or substitutions: new ideas for old, new labor patterns for old, new technologies for old. The diffusion of new technologies follows common patterns that guide the selection of technologies and their rate of adoption in the human environment.
We are all accustomed to the idea of growth to a limit, logistic growth described graphically by an S-shaped curve; for example, the number of people becoming ill in an epidemic that grows rapidly before eventually reaching a plateau. In fact, observers have recorded thousands of examples of such S-shaped growth in settings as diverse as animal populations, energy, and transport infrastructures, language acquisition, and technological performance. Typically, the variable representing a population or system development and diffusion (species population, plant height, engine power, microchip capacity) grows exponentially at the outset. However, such systems whether natural or man-made cannot sustain exponential growth indefinitely. Negative feedback mechanisms or signals from the environment slow the growth, producing the S-shaped curve.
For a single growth process, a single sigmoidal curve is often a useful model. In niches or markets in which several populations or technologies compete, the growth and decline of each entry also often exhibit logistic behavior. This behavior depends on interactions among the competitors. Namely, if a technology’s market share grows, it comes at the cost of shares of others. This process is well-described by the so-called “logistic substitution model.”
The logistic model also finds applications in demography, notably to model transitions in fertility. For example, in 2009 PHE researchers conducted a demographic study projecting population for the globe as well as individual countries in the year 2050 based on a logistic model of fertility. See ‘Implosions, explosions: Population projections to 2050 based simply on a logistic model of fertility‘
To offer guidance for considering the diffusion of technologies that affect the human environment, the PHE explores the factors determining when socio-technical diffusion succeeds and how its speed and extent change over time. As part of this effort to advance and ease analyses of logistic behavior in time-series data, the PHE has developed the “LogletLab” software package to fit logistic curves and apply the logistic substitution model to single as well as multiple time-series data sets.
LogletLab 4, launched in 2017, expanded functionality of the platform to allow users to employ a range of statistical tools to analyze data sets. The software has been used to perform countless new analyses examining the limits of human physical and cognitive performance, human migration, and the diffusion of human disease among other phenomenon.
To see LogletLab 4 click here.
LogletLab 5 is now available. We welcome suggestions for better functionality and new or improved features.
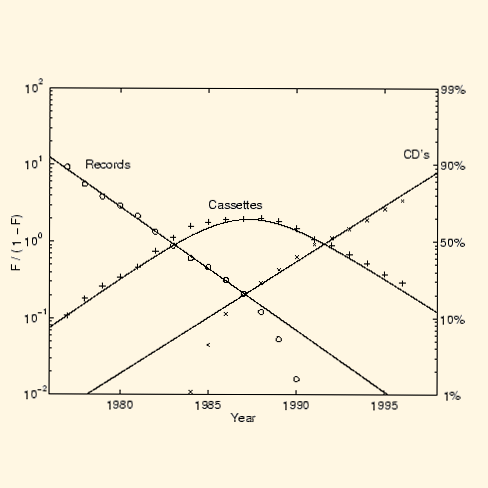
About the icon – Chart shows the Logistic Substitution of US Music Recording Media 1977-1996.
Publications about Diffusion of Social Phenomena
. Jewish population trajectories between the Jordan River and the Mediterranean Sea [external link]. Israel Affairs vol. DOI: 10.1080/13537121.2023.2206247, 2023
. Peak Human? Thoughts on the Evolution of the Enhancement of Human Performance (PDF). Pp. 20 in Program for the Human Environment, The Rockefeller University, 2023
. Trajectories of COVID-19: A longitudinal analysis of many nations and subnational regions [external link]. PLOS ONE 2023
. The Virtual Worlds of Climate and Energy [external link]. RealClear Energy vol. August, 2023
. Moore’s Law revisited through Intel chip density [external link]. PLOS ONE 16 (8): e0256245, 2021
. Microphysics and Macrohistory (PDF). Looking Back as we Move Forward: The Past, Present and Future of the History of Science 2019
. The Potato and the Prius (PDF). 2018 Keynote address to the 2018 Potato Business Summit of the United Potato Growers of America, Orlando, FL, 10 January 2018.
. Jews in Time and Space (PDF). International Journal of Anthropology 31 (1-2): 93–109, 2016
. Quantitative Dynamics of Human Empires [Color Booklet Version, 52 pages] (PDF). Adapted from Marchetti and Ausubel, International Journal of Anthropology 27(1-2):1-62, 2012. 2013
. Quantitative Dynamics of Human Empires (PDF). International Journal of Anthropology 27 (1-2): 1–62, 2012 Empires; territory; logistic growth; testosterone; progesterone
. Will the Rest of the World Live Like America? (PDF). Technology in Society 26 (2004): 343–360, 2004 Zipf, golden ratio, inequality, sustainable development
. The Next 1000 Years (PDF). 2003 Discussion paper for April 2003 Rockefeller U workshop
. DRAMs as model organisms for study of technological evolution (PDF). Technological Forecasting and Social Change 69 (3): 243–262, 2002 Technological substitution; Learning curves
. Death and the Human Environment: The United States in the 20th Century (PDF). Technology in Society 23 (2): 131–146, 2001 Mortality, epidemiological transition, morbidity
. A primer on logistic growth and substitution: The mathematics of the Loglet Lab software (PDF). Technological Forecasting and Social Change 61 (3): 247–271, 1999 Logistic curve model
. Carrying Capacity: A Model with Logistically Varying Limits (PDF). Technological Forecasting and Social Change 61 (3): 209–214, 1999 Carrying Capacity, Growth Models, Logistic Model
. Loglet Lab for Windows (version 1.1) Tutorial (PDF). Technological Forecasting and Social Change 61 (3): 273–295, 1999 Logistic curve model
. Elektron: Electrical Systems in Retrospect and Prospect Pp. 110–134 in Technological Trajectories and the Human Environment, . Washington, DC: National Academy Press, 1997 Also appeared in Daedalus 125(3):139-169, Summer 1996. energy, electric power
. Human Population Dynamics Revisited with the Logistic Model: How Much Can Be Modeled and Predicted? Pp. 1–30 in Technological Forecasting and Social Change vol. 53, 1996 Logistic curve model, population
. Bi-Logistic Growth Pp. 89–102 in Technological Forecasting and Social Change vol. 47, 1994 Logistic curve model
. Graphical representation of the world population growth (PDF). Human Dimensions Quarterly 1 (2): 17–19, 1994 population, logistic curve model
. Rat Race Dynamics and Crazy Companies: The Diffusion of Technologies and Social Behavior (PDF). Pp. 11–22 in Technological Forecasting and Social Change vol. 39, 1991 technology diffusion
. Regularities in technological development: An environmental view [external link]. Pp 70-91 in J.H. Ausubel and H.E. Sladovich, eds.Technology and Environment, National Academy, Washington DC 1989 technology diffusion, logistic model curve