Numerical methods for logistic substitution

Now we present the mathematical methods used by the logistic substitution modeling engine.

Suppose we have $n$ technologies competing in a market over the course of $m$ years. Our data representation now becomes a set of $n$ vectors of length $m$, or an $n \times m$ matrix. To proceed with the model, the first step is to transform the raw data, $d_{ij}$, into fractional shares $Fr_{ij}$ of the market:

$$Fr_{ij} = \frac{d_{ij}}{\displaystyle {\sum^{n}_{k = 1}{d_{kj}}}}$$

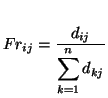
Secondly, the fractional shares $Fr_i$ are transformed using the previously described Fisher-Pry transform

$$FR_{ij} = FP(Fr_{ij}) = \frac{Fr_{ij}}{1 - Fr_{ij}}.$$

Recall that under the Fisher-Pry transform, an S-shaped logistic becomes a straight line when plotted on a semi-log graph; data which grow (or decline) logistically will appear to grow (or decline) linearly when transformed.

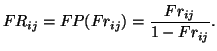
The logistic substitution model generates substitution curves, $L_1, L_2, \dots, L_n$, that correspond to the fractional market share data $Fr_1, Fr_2, \dots, Fr_n$. The smooth curves follow the market share through the three substitution phases: logistic growth, non-logistic saturation, and logistic decline.

The first step in generating these curves from the logistic substitution model is to fit a curve to the growth phase of each technology. (Alternatively, as when data for the growth phase is unavailable for a particular technology, we fit a curve to its decline phase.) Reiterating from above, because we are working in the Fisher-Pry transform space, then

$$\ln\frac{L_i}{1 - L_i} = - \frac{\ln 81}{\Delta t_i}(t-t_{mi})$$

is linear, and we can estimate the parameters for such a curve with linear regression. As before, $\Delta t_i$ is the characteristic growth time for the $i$th technology, and $t_{mi}$ is the midpoint of the $i$th technology's period of growth or decline.

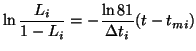
Note that for the logistic substitution model, we use a logistic with only two parameters, because the third parameter, saturation level, $\kappa$, has fixed at 1, or 100%. Without the introduction of a new technology, the last technology in the growth phase would grow to a 100% market share. If a new technology is introduced, its growth must come at the cost (primarily) of the leading technology, causing it it to saturate and decline.

For each technology, it is necessary to specify the time window that represents its logistic growth (or decline). Within this time window are the data that will be used to estimate the parameters for the logistic that we just described. Figure 10 shows the logistic substitution model for the recording media data. The years 1975 to 1985 were used to estimate the logistic decline phase of LP's. The years 1977 to 1985 were used to model the logistic growth phase of cassettes. The years 1988 to 1996 were used to estimate the parameters for the logistic growth phase of CD's.

The growth and decline phases can be represented by logistic curves, but this is not the case for the saturation phase. Because only one technology, $L_s$, can be saturating at a time, its market share can be calculated by subtracting the sum of the shares of all the other technologies-which must be known, since they must be either growing or declining-from unity (100%):

$$L_{s} = 1 - \sum_{i \neq s} L_i.$$

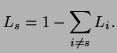
How do we know when each phase begins or ends? If

$$y_s(t) = \ln \frac{L_s (t)}{1-L_s (t)} ,$$

then the termination of the saturation phase comes at time $t$ at which

$$\frac{y_s''(t)}{y_s'(t)}$$ (9)

When the saturation phase for a technology ends, it proceeds directly into its decline phase, and the saturation phase for the next technology immediately commences. The two parameters for the logistic decline phase of the curve are given by:

$$\Delta t_s = \frac{\ln(81)}{y_s'(t)}$$

$$t_{ms} = \log\frac{(y_s(t) - \frac{ln(81)}{\Delta t} t)}{\frac{\ln(81)}{\Delta t}}$$

Figure 10: Logistic Substitution of US Music Recording Media. Source of data:[18].

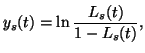
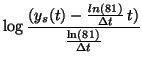Figure 10 shows the logistic substitution model for U.S. recording media. In this example, the LP's are in the logistic decline phase, cassettes are in transition, and CD's are in logistic growth.