Area of Research: Diffusion of Social Phenomena

This paper first appeared in the journal Technological Forecasting and Social Change, published by Elsevier Science Inc., New York.

Introduction

Many processes in biology and other fields exhibit S-shaped growth. Often the curves are well modeled by the simple logistic growth function, first introduced by Verhulst in 1845. Although the logistic curve has often been criticized for being applied to systems where it is not appropriate, it has proved useful in modeling a wide range of phenomena. Kingsland [1] provides a thorough history of the applications of the simple logistic curve in population ecology, its successes and failures. Marchetti and colleagues at IIASA [2,3], as well as many others [4], have shown thousands of examples, mainly in socio-technical systems. Recently, Young [5] surveyed and compared growth curves used for technological forecasting, including the logistic function. Almost all the analyses and successes apply to the case of a single growth process operating in isolation. Here, I extend the analysis of logistic functions to cases where dual processes operate.

The carrying capacity of a human system is often limited by the current level of technology, which is subject to change. More generally, species can sometimes alter and expand their niche. If the carrying capacity of a system changes during a period of logistic growth, a second period of logistic growth with a different carrying capacity can superimpose on the first growth pulse. For example, cars first replaced the population of horses but then took on a further growth trajectory of their own. We call such a system with two logistic growth pulses, growing at the same time or sequentially, “Bi-logistic.” As I will show, the Bi-logistic is useful in modeling many systems that contain complex growth processes not well modeled by the simple logistic.

The plan of this paper is as follows. First, a model based on the sum of two simple logistic growth pulses is presented in order to analyze systems that exhibit Bi-logistic growth. A nonlinear least-squares algorithm is described that allows values for the model parameters to be estimated from time-series growth data. Then, model sensitivity and robustness are discussed in relation to error structure in the data. Finally, a taxonomy and examples of systems that exhibit Bi-logistic growth are discussed.

Logistic Growth

The logistic law of growth assumes that systems grow exponentially until an upper limit or “carrying capacity” inherent in the system is approached, at which point the growth rate slows and eventually saturates, producing the characteristic S-shape curve [6]. In the simple exponential growth model, the growth rate of a population, N(t), is proportional to the population

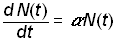
.(1)

As a consequence, there are no limits to growth; as t® ¥, N(t)® ¥. In the familiar analytic form, a is a growth rate parameter and b is a location parameter that shifts the curve horizontally but does not alter its shape:

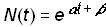
(2)

The logistic model adds to the exponential model (1) a feedback term that slows the growth rate of the system as the “carrying capacity” or saturation parameter k is reached

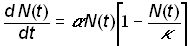
(3)

For values of N(t) << k, equation (3) closely resembles exponential growth. As the population N(t) approaches k, the feedback term causes the rate of growth to slow to zero, giving rise to the familiar symmetrical S-shaped curve. The logistic law of growth arises as a solution to equation (3)

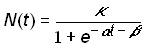
(4)

where a is a rate parameter; b is a location parameter (it shifts the function in time but does not affect the function’s shape); and k is the asymptotic value that bounds the function and therefore specifies the level at which the growth process saturates [7]. Symmetry implies that the logistic function has a point of inflection at k/2. It is convenient to define t_m as the midpoint of the growth process: N(t_m) = k/2. The location parameter b can be replaced by t_m by defining b = -t_ma. It is also convenient to define a parameter Dt as the length of the time interval required for the growth process to grow from 10 to 90 percent of the saturation level k. The length of this interval (derived through simple algebra) is Dt = (ln81)/a.

An equivalent form of the standard 3-parameter logistic model (4) with parameters convenient for the analysis of historical time-series data can be defined as

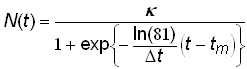
.(5)

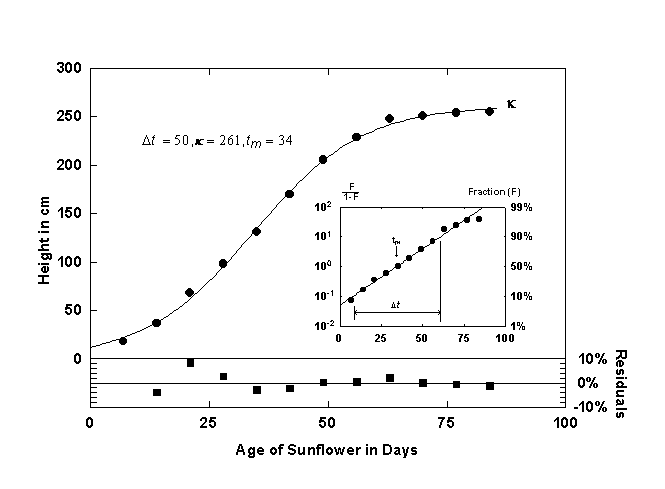
Figure 1. Growth of a sunflower fitted with a single logistic curve. The inset shows the logistic curve and the data linearized with the Fisher-Pry transform. The lower panel shows the residuals in percent deviation from the fitted curve. Source of data: [8].

Figure 1 shows the growth of a sunflower [8] and the corresponding logistic curve. The residuals (in percent deviation) are plotted in t he panel beneath the logistic curve.

The logistic growth curve can be linearized by a change of variable (first discussed by Fisher and Pry [9]), by defining

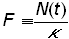
(6)

and substituting into equation (4)

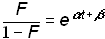
.(7)

Plotting equation 7 with a logarithmic y-axis produces a straight line, and Dt and t_m can be easily read off this plot if the corresponding percents of saturation are marked. Plotting the logistic linearly also facilitates the rapid comparison to other logistic growth processes because all the curves are normalized by k. The inset of Figure 1 shows the sunflower data and the corresponding logistic curve plotted linearly. If k is known, the parameters Dt and t_m can be determined by using a linear regression technique to fit a straight line through the transformed data.

As discussed, the logistic growth model has been successfully applied to a wide range of biological and socio-technical systems. To explain why the logistic is so pervasive, Montroll [10] postulates “laws” of social dynamics modeled after Newton’s laws of particle dynamics. The first law of social dynamics states that “in the absence of any social, economic, or ecological force, the rate of change of the logarithm of a population, N(t), of an ‘organism’ is constant”,

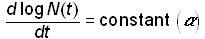
.(8)

This is equivalent to Newton’s first law, which states that a particle in motion in the absence of any external forces will travel in a straight line with constant velocity. Equation (8) is also equivalent to exponential growth.

Montroll’s second law of social dynamics states that equation (8) is violated when a social, economic, or ecological force is applied. One of the simplest “forces” that could replace the right-hand side of equation (8) is a linear force proportional to the population:

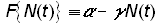
(9)

which represents a deterrence to population growth. If g is replaced by a/k, where k is the carrying capacity, equation (8) becomes

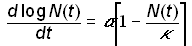
(10)

which is equivalent to the logistic model (3). Thus, logistic growth can be viewed as a canonical form of growth for a system that is subject to forces that slow unconstrained growth. If multiple forces operate, a system can undergo more than one logistic growth pulse, as will be discussed shortly.

Bi-Logistic Growth

The standard 3-parameter form of the logistic growth model describes one period or “pulse” of growth as the system proceeds from rapid exponential growth to slow growth as the carrying capacity k is approached. Multiple growth pulses characterize many systems. In the case of a system with two well-defined serial logistic growth pulses, it is possible to split the time-series data set in two and model each set with a separate 3-parameter logistic function. This method is limited because it is often unclear exactly where to split the data set. Cases appear rare where one process ends entirely before the second begins. Problems arise in assigning values from the “overlap” period to the first or second pulse.

A superior alternative is to analyze systems that exhibit Bi-logistic growth by using the time-series data to estimate the parameters of a model comprised of the sum of two 3-parameter logistic growth pulses. The Bi-logistic growth model is then

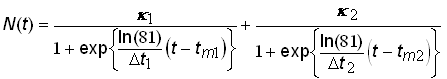
.(11)

Selection of a method to estimate the parameters depends on the assumed distribution of the measurement errors in the data. A standard procedure is to assume that the measurement errors are independently and normally distributed with constant standard deviation. The best-fit parameters can then be found by minimizing the sum of the squares of the residuals. The residuals are defined as the difference between the time series data set (t_i,y_i) with m data points and the Bi-logistic model N(t)

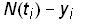
Residuals = i = 1…m(12)

The parameter estimates can then be found by using a nonlinear regression technique to minimize the sum of the squares of the residuals

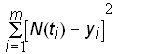
Minimize(13)

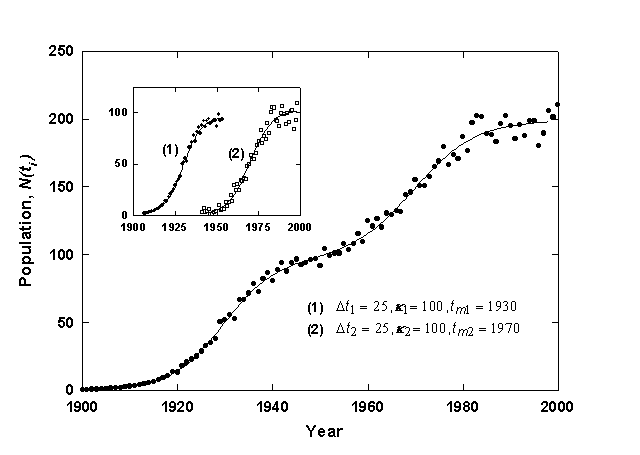
Figure 2. Example of a Bi-Logistic growth curve generated with 3% relative Gaussian error. The inset shows component growth curves.

The measurement errors of many historical data sets are unknown. Thus the common assumption that the errors are independently and normally distributed is often invalid. A least-squares method of regression can still be used to estimate parameters for these data sets, but the estimates are no longer guaranteed to be unbiased. When the measurement errors of a time series data set are unknown, as in the examples presented later in this paper, an ordinary least-squares regression technique, which gives equal weight to all of the data points, may be preferable.

In the following analyses, the Levenberg-Marquardt (L-M) method [11] of nonlinear least-squares regression is used to estimate the 6 parameters of the Bi-logistic function (11). The L-M algorithm requires provisional estimates to initiate its search for the parameters. That is, some a priori or external knowledge of the system is needed to derive estimates reasonably and efficiently. Usually, simple visual examination of the plotted raw data suffices. The L-M implementation used allows any number of the 6 parameters to be held at a constant value (if, say, the carrying capacity of a system is known). This feature also facilitates the derivation of initial parameters, because the regression routine has better convergence properties when fewer parameters are estimated.

Figure 2 shows a generated time-series data set fit with a Bi-logistic curve. The data set is the sum of two identical logistic growth pulses with the midpoints (t_m) separated by 40 years. The first pulse has reached 90% of saturation (k₁) before the second pulse begins, and thus two overlapping S-shaped curves are visible. Once the fit is obtained, a simple deconvolution can be defined as follows

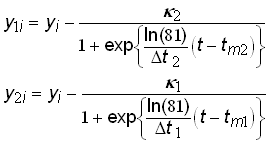
(14)

where y_1i and y_2i are the component growth variables, which are plotted in the inset of figure 2.

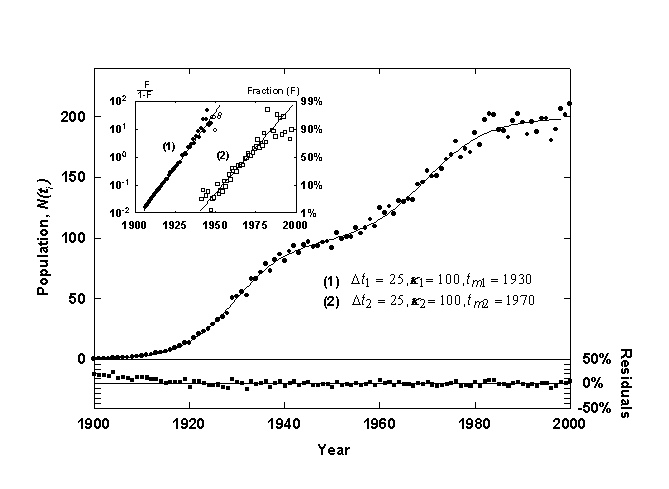
Figure 3. Example of a Bi-Logistic growth curve generated with 3% relative Gaussian error. The inset shows the component growth curves linearized with the Fisher-Pry transform. The lower panel shows the residuals from the fit in percent deviation from the fitted curve.

The two data sets (t_i, y_1i) and (t_i, y_2i), can also be plotted as a linear function of time by utilizing the Fisher-Pry transform, as shown in the inset of Figure 3, with the circles designating (t_i, y_1i) and the squares designating (t_i, y_2i). When the second logistic pulse is below 1% of saturation (k₂), the first component data set (t_i, y_1i>) is essentially identical to the raw data, (t_i, y_i), and it is plotted with solid circles. After this, the data are plotted with open circles to indicate that the data have been transformed. The second component growth data set (t_i, y_2i) is plotted with hollow squares to indicated that these data have also been transformed. The linear form of the Bi-logistic facilitates morphological analysis and comparison to other Bi-logistic processes.

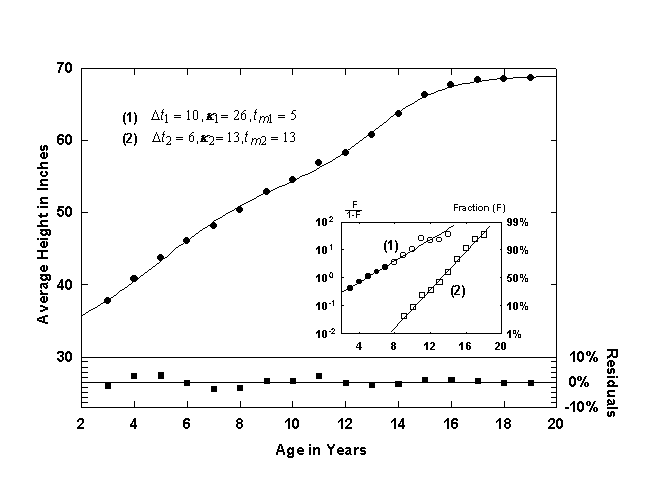
Figure 4. Average height of American Boys with a Bi-Logistic growth curve. Note that the Bi-logistic curve is offset by 30 inches in order to account for early growth (ages 0 to 3). Source of data: [12].

A well-known growth process involving two growth spurts is shown in Figure 4, the average height of boys ages 3 to 19, in this case, American [12]. Two S-shaped growth pulses are clearly visible. The first growth pulse shown is centered at 5 years and has a characteristic growth time, Dt, of 10 years. The second growth pulse, called the “prepubertal acceleration” or the “adolescent spurt” is shorter and is centered at 13 years old. This growth pulse saturates at 68.7 inches, the average height of American men. The inset shows the Fisher-Pry linear transform of the two growth pulses.

The residuals are useful in determining how well the Bi-logistic model fits the data. If a system is well modeled by the Bi-logistic function, then the residuals will contain only noise, and the residuals will be randomly distributed around zero. The residuals can also tell a lot about the error structure. The lower part of Figures 3 and 4 show the residuals of the fit on the two time-series data. The residuals are shown as the percent deviation from the estimated value

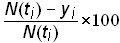
residuals in percent deviation =.(15)

Many time series data sets from systems that are studied with logistics contain error that is relative to the growth level, which can change by orders of magnitude in the duration of the process. Accordingly, it is useful to analyze the residuals in percent deviation. While the ordinary least-squares technique used for analysis assumes constant error variance, it might be advantageous to use a regression method that assumes constant relative error, thus weighing the early growth data more heavily than the later data. However, early growth data are often unreliable, as processes may also not be well recorded or established. Thus there is a trade off between assuming relative error and constant error. The effect can be seen in the comparatively high levels of error present in the early data on the residual plot of the generated time-series data (figure 3), which was fit assuming constant error. More research is needed to determine the error structure of historical data-sets and on regression techniques that yield the best parameter estimates. Monte-Carlo techniques could be used to generate sample data sets with different error structures, and the subsequent analysis would be useful in determining confidence intervals for the Bi-logistic model parameters. Residual analysis could also identify “slices” of data that are especially noise-free and might be more heavily weighted when fitting.

Taxonomy of the Bi-logistic

A continuous spectrum of curves can be generated from the Bi-logistic model. However, it is useful to distinguish four basic patterns of Bi-logistic growth in order to develop a taxonomy of curves that can be used as a reference when analyzing systems where the shapes of the two underlying logistic trends are not already known. As mentioned, the regression routine used requires initial estimates, and a taxonomy is useful in this regard.

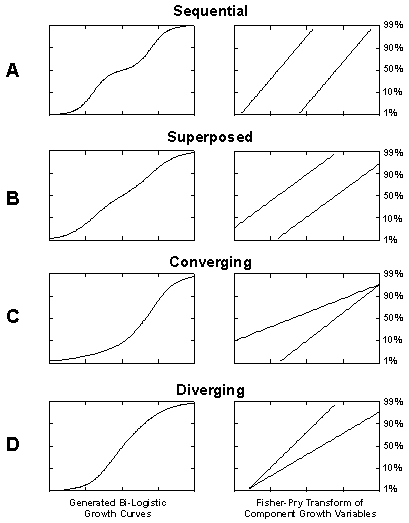
Figure 5. Taxonomy of the Bi-logistic growth model.

Figure 5 shows four hypothetical curves and their linearized versions.

Curve A of Figure 5 shows a Bi-logistic curve with two almost non-overlapping logistic growth pulses, dubbed the “sequential logistic”. The second pulse does not start growing until the first pulse has reached about 99% of saturation k₁. This shape Bi-logistic characterizes a system which pauses between growth phases.

The B curve shows a Bi-logistic where the second pulse starts growing when the first pulse has reached about 50% of saturation. This “superposed” Bi-logistic growth model characterizes systems that contain two processes of a similar nature growing concurrently except for a displacement in the midpoints of the curves.

Curve C shows a growth process where a first pulse of logistic growth is joined by a second faster pulse, dubbed the “converging” logistic model, as the two pulses culminate about the same time. Often an advance in technology will allow both the carrying capacity and the growth rate of a system to increase, causing the second pulse to rise from the first with both a faster characteristic Dt, and higher carrying capacity,k.

Curve D shows a “diverging” Bi-logistic curve where two logistic growth processes begin at the same time but grow with different rates and carrying capacities defined from the start. It is noteworthy that curves C and D are S-shaped but asymmetric. They do not “look logistic.”

Examples and Results

A wide variety of historical time-series data sets were analyzed with the Bi-logistic model. The data sets exhibited here show the four types of Bi-logistic growth described above. The data sets chosen all show growth processes that have neared saturation in order to permit analysis of the residuals for the entire growth process. The data sets were also fitted with a single logistic growth pulse to check the improvement in fit by the Bi-logistic.

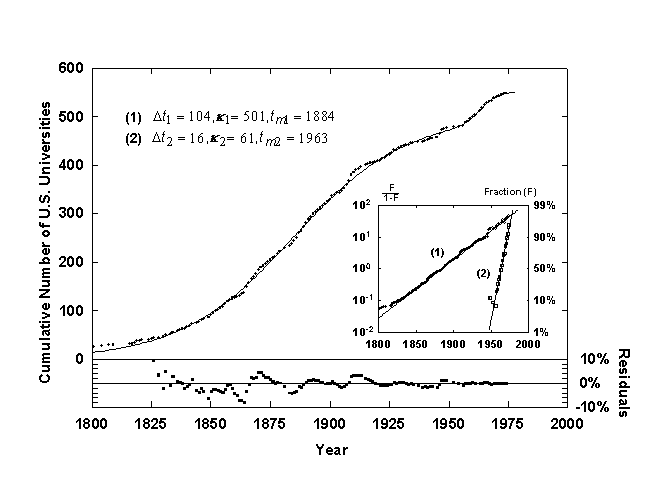
Figure 6. Growth of U.S. universities with a Bi-Logistic growth curve. Source of data: [13].

A sequential Bi-logistic is shown in figure 6, the growth of U.S. universities since 1700, as tabulated from the founding dates provided in Webster’s New Collegiate Dictionary [13]. The first pulse saturates at a k of 500 universities with the point of inflection and fastest rate of growth, t_m, occurring in 1885. This is when many states inaugurated their public university systems. The second, smaller logistic pulse starts in 1950 when the first pulse has reached about 95% of saturation and has a much quicker characteristic growth time, Dt, of about 15 years. This pulse represents largely the creation of additional daughter campuses of state universities, a smaller niche to fill than the founding of universities for the U.S. as a whole.

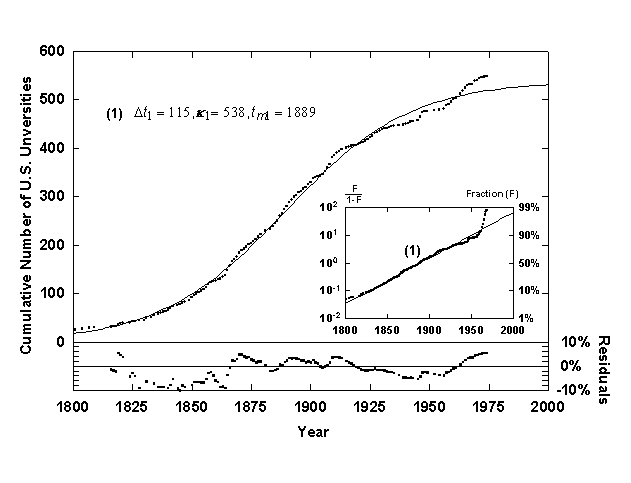
Figure 7. Growth of U.S. universities with a single logistic growth curve. Source of data: [13].

To indicate the superiority of the Bi-logistic, consider Figure 7, which shows the same university data fitted with a single logistic curve. Optical inspection of the fitted curve as well as analysis of the residuals show that the Bi-logistic model fits the data much better than a single logistic curve. The residuals of the early data (1600-1800) have small absolute error but because the growth level is low the percent error is very high (~100%). As mentioned, this deviation is caused in part by the non-weighted regression algorithm used. The early growth of systems (below 10% of final saturation) is also suspect because feedback mechanisms that are assumed for logistic growth might not be in place yet, and thus the growth is probably not firmly logistic until a growth level of about 10% of the final saturation value has been reached.

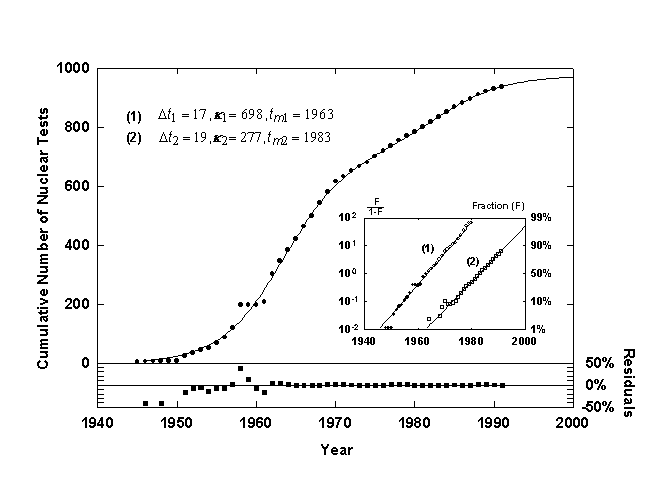
Figure 8. U.S. nuclear weapons tests with a Bi-logistic growth curve. Source of data: [14].

Figure 8 shows the cumulative number of U.S. nuclear weapons tests [14] with a superposed Bi-logistic curve. The Bi-logistic provides an excellent fit, as shown by the residuals. The fastest rate of growth of the first pulse occurred in 1963, following the Cuban missile crisis. While the first logistic pulse was largely the race to develop bombs with higher yields, the second pulse, centered in 1983 and nearing saturation now, is probably due to research on reliability and specific weapons designed for tactical use. The Bi-logistic model predicts that we are at 90% of saturation of the latest pulse. Processes often expire around 90%, though sometimes processes overshoot. The residuals show the extraordinary, deviant increase in U.S. tests after the scare of the 1957 sputnik launch.

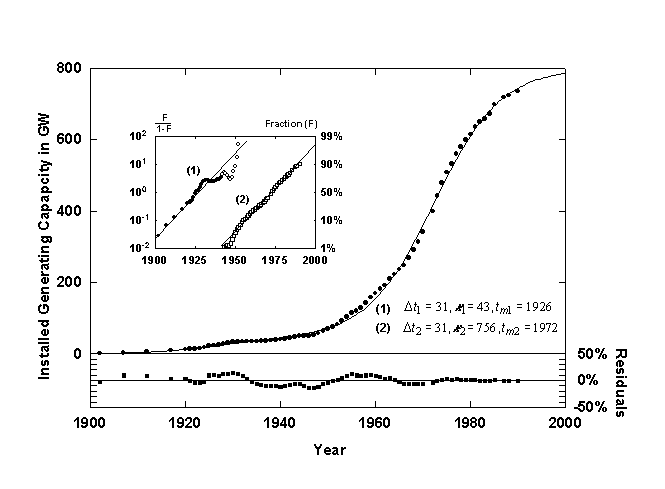
Figure 9. U.S. installed electric generating capacity with a Bi-logistic growth curve. Source of data: [15, 16].

Figure 9 shows the U.S. installed electric generating capacity [15,16] with a converging Bi-logistic curve. The first logistic pulse saturates at about 43 GW and is centered in 1926. A second shorter but much higher pulse begins in about 1940 and is at about 90% of saturation now. Ausubel and Marchetti [17] provide a detailed analysis of the underlying mechanisms affecting the electrification of the U.S. The first pulse of growth is associated with pure substitution, for example, the replacement of water mills and gaslight by more efficient and convenient electric devices. The second and much larger growth pulse is due to the increase in demand of electricity for energy functions that could not be easily fulfilled before electrification, ranging from TV’s to space cooling. The pair of pulses have more or less saturated now. A third electric pulse might be starting with the rapid increase in demand for information handling and new concepts in electric transport.

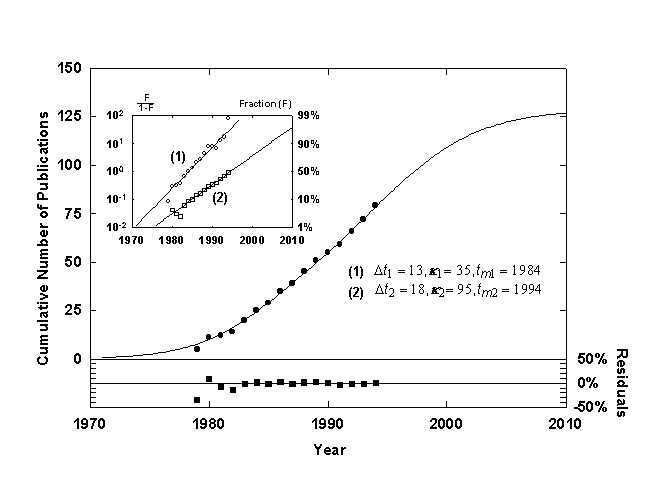
Figure 10. Cumulative number of published works, Jesse H. Ausubel, with a Bi-logistic growth curve. Source of data: personal communication.

Figure 10 shows the cumulative number of publications written or edited by my colleague, Jesse H. Ausubel, fitted with a diverging Bi-logistic curve. The first smaller, steeper pulse consists of committee reports and other collective documents associated with his work as a staff officer and study director. The second longer and higher pulse consists of research papers of which Ausubel is an author. His dual professional career is made neatly apparent by the Bi-logistic.

Issues and Conclusion

To analyze time series data sets where the simple logistic curve provides a poor fit, many other growth models have been examined [18] , such as the Gompertz function. These data sets might contain multiple growth pulses that would be better modeled by the Bi-logistic. Some of the other models introduce higher-order parameters where the physical interpretation is less clear than in the case of the Bi-logistic. More research is needed in order to determine if the Bi-logistic model performs as well as more complex non-symmetrical growth functions. Complex systems can also undergo or consist of more than two pulses of growth, and research is needed into the feasibility of extending the Bi-logistic model into an arbitrary sum of simple logistics. Of course, with enough parameters anything can be fit.

The logistic growth function has proven useful in modeling a wide variety of phenomena in the growth of systems. However, complex systems rarely follow a single S-shaped trajectory. The Bi-logistic function is effective in modeling systems that contain two logistic growth pulses. The Bi-logistic is attractive because it is a parsimonious model to which we can still attach clear physical interpretations.

Acknowledgments: I am grateful to Jesse Ausubel, John Helm, Robert Herman, Arnulf Grübler, Cesare Marchetti, Nebojsa Nakicenovic, and Andy Solow for advice and assistance.

References

1. Kingsland, S., The Refractory Model: The Logistic Curve and the History of Population Ecology, The Quarterly Review of Biology 57, 29-52 (1982).
2. Marchetti, C., Branching out into the Universe, in Diffusion of Technologies and Social Behavior, N. Nakicenovic and A. Grübler, eds., Springer-Verlag, New York, NY, 1991.
3. Grübler, A., The Rise and Fall of Infrastructures, Springer-Verlag, New York, NY, 1990.
4. Oliver, R. M., Saturation Models: A Brief Survey and Critique, Journal of Forecasting (Special Issue on Predicting Saturation and Logistic Growth) 7, 15-255 (1988).
5. Young, P., Technological Growth Curves: A Competition of Forecasting Models, Technological Forecasting and Social Change 44, 375-389 (1993).
6. Stone, R., Sigmoids, Bulletin in Applied Statistics 7, 59-119 (1980).
7. Nakicenovic, N., U.S. Transport Infrastructures, in Cities and Their Vital Systems, J. Ausubel and R. Herman, eds., National Academy Press, Washington, D.C., 1988.
8. Reed, H.S. and Holland, R. H., The Growth of an Annual Plant Helianthus, Proceedings of the National Academy of Sciences (USA), 5, 135-144 (1919).
9. Fisher, J.C., and Pry, R. H., A Simple Substitution Model of Technological Change, Technological Forecasting and Social Change 3, 75-88 (1971).
10. Montroll, E. W., Social Dynamics and the Quantifying of Social Forces, Proceedings of the National Academy of Sciences (USA) 75(10), 4633-37 (1978).
11. Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P., Numerical Recipes in C: The Art of Scientific Computing 2nd ed., Cambridge University Press, New York, NY, 1992.
12. Krogman, W. M., Child Growth, University of Michigan Press, Ann Arbor, MI, 1972.
13. Woolf, H. B., ed., Webster’s New Collegiate Dictionary, Merriam-Webster, Springfield, MA, 1979.
14. Stockholm International Peace Research Institute Yearbook 1992, Oxford University Press, New York, 1992.
15. U.S. Bureau of the Census, Historical Statistics of the United States, Washington, D.C., 1975.
16. U.S. Bureau of the Census, Statistical Abstract of the United States, Washington, D.C., (Various Years).
17. Ausubel, J. and Marchetti, C., Elektron, Forthcoming in Technological Trajectories and the Human Environment, J. Ausubel and D. Langford, eds., National Academy Press, Washington, D.C.
18. Posch, M., Grübler, A., and Nakicenovic, N., Methods of Estimating S-Shaped Growth Functions, International Institute for Applied Systems Analysis, Laxenburg, Austria, 1987.