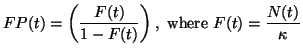Next: Bi- and multi-logistic curves
Up: The Component Logistic Model
Previous: The Component Logistic Model
Contents
There are many ways to visualize logistic growth aside from simple
plotting on a linear scale. It is possible to define a change of
variables that normalizes a logistic curve and renders it as a
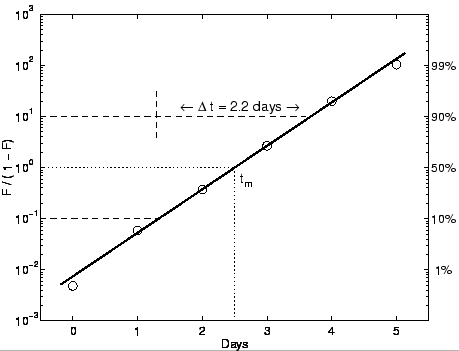
straight line (see Figure 2). This view is known as the Fisher-Pry3 Transform:
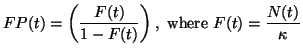 |
(3) |
Figure 2:
The logistic growth of a bacteria colony plotted using the Fisher-Pry
transform that renders the logistic linear.
|
|
Note that
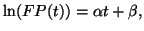 |
(4) |
so if 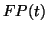 is plotted on a logarithmic scale, the S-shaped logistic is
rendered linear. We observe that the time in which the range is
between
is plotted on a logarithmic scale, the S-shaped logistic is
rendered linear. We observe that the time in which the range is
between 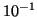 and
and 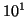 is equal to
is equal to 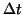 , and the time
at
, and the time
at 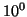 is the point of inflection (
is the point of inflection (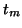 ). Moreover,
because the Fisher-Pry transform normalizes each curve to the carrying
capacity
). Moreover,
because the Fisher-Pry transform normalizes each curve to the carrying
capacity 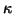 , more than one logistic can be plotted on the same
scale for comparison. As we will see, this becomes particularly
useful when we analyze more complex growth behaviors. Figure 2
shows the Fisher-Pry transform of the bacteria example in figure 2. On
the right axis we label the corresponding percent of saturation (
, more than one logistic can be plotted on the same
scale for comparison. As we will see, this becomes particularly
useful when we analyze more complex growth behaviors. Figure 2
shows the Fisher-Pry transform of the bacteria example in figure 2. On
the right axis we label the corresponding percent of saturation ( 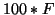 ) at each
order of magnitude from
) at each
order of magnitude from 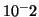 to
to 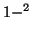 rounded to the nearest percent.
rounded to the nearest percent.




Next: Bi- and multi-logistic curves
Up: The Component Logistic Model
Previous: The Component Logistic Model
Contents
Jason Yung
2004-01-28