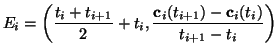Next: Residuals
Up: The Mathematics of Loglet
Previous: Decomposition
Contents
Growth rates and the ``bell'' view
Just as the differential equation (1) reveals the
mechanism propelling its integral equation (2),
the rates of change of the component logistics provide clues to the
mechanisms propelling the composite logistic. Analyzing the rates of
change is often useful when yearly or percent per year tabulations
are applicable, as in the case of economic data. Recall
that the analytic form of the three-parameter logistic is:
The instantaneous rate of growth of the
logistic function is given by its derivative with respect to time:
![$\displaystyle \frac{d N(t)}{d t}= \frac{\frac{\ln(81)}{\Delta t} \kappa \...
...1 + \text{exp} \left( {-\frac{\ln(81)}{\Delta t}}(t -t_{m}) \right) \right]^2 }$](img77.png) |
(8) |
Figure 6:
The rates of change of the component logistics
(``The Bell View'')
|
|
Plotting (8) produces a bell-shaped curve
similar, but not identical, to the normal distribution
function. Naturally, the bell-shaped curve peaks at the midpoint
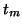 ; analytically, this is the point of inflection, and thus it is
an extremum of
; analytically, this is the point of inflection, and thus it is
an extremum of 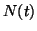 . Panel B of Figure 6 shows the
derivative of the component logistics of our test function (Panel A is
shown again for comparison purposes).
. Panel B of Figure 6 shows the
derivative of the component logistics of our test function (Panel A is
shown again for comparison purposes).
The rate of change of the data subsets 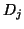 is computed discretely,
creating the sets
is computed discretely,
creating the sets
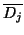 , in which each point
, in which each point 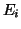 is
is
where
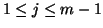 . In other words,
. In other words, 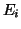 contains the
discrete derivative from
contains the
discrete derivative from
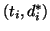 to
to
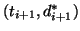 .
.
Loglet Lab can decompose a logistic curve into its discrete components;
each component can be transformed using the Fisher-Pry transform,
or their rate of change can be plotted.




Next: Residuals
Up: The Mathematics of Loglet
Previous: Decomposition
Contents
Jason Yung
2004-01-28
![$\displaystyle N(t)= \frac{\kappa}{1 +
\text{exp} \left[ {-\frac{\ln(81)}{\Delta t}}(t -t_{m}) \right] }
$](img76.png)
![$\displaystyle N(t)= \frac{\kappa}{1 +
\text{exp} \left[ {-\frac{\ln(81)}{\Delta t}}(t -t_{m}) \right] }
$](img76.png)
![]() ; analytically, this is the point of inflection, and thus it is
an extremum of
; analytically, this is the point of inflection, and thus it is
an extremum of ![]() . Panel B of Figure 6 shows the
derivative of the component logistics of our test function (Panel A is
shown again for comparison purposes).
. Panel B of Figure 6 shows the
derivative of the component logistics of our test function (Panel A is
shown again for comparison purposes).
![]() is computed discretely,
creating the sets
is computed discretely,
creating the sets
![]() , in which each point
, in which each point ![]() is
is