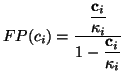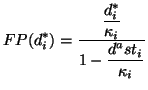Next: Growth rates and the
Up: The Mathematics of Loglet
Previous: Definitions and notation
Contents
Now consider the set of 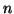 logistic components
logistic components
 ,
where
,
where
where 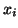 is an arbitrary subspace of
is an arbitrary subspace of 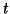 . (The components
. (The components 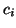 are analogous to
are analogous to 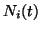 as discussed in equation
(7).) A typical choice for
as discussed in equation
(7).) A typical choice for 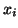 is the interval
over which
is the interval
over which 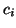 grows from 10% to 90% of its saturation level,
namely
grows from 10% to 90% of its saturation level,
namely
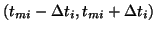 .
.
Restricting the domain of 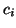 gives us a criterion for
decomposing the associated data set
gives us a criterion for
decomposing the associated data set 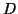 into subsets
into subsets 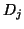 (
(
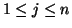 ) corresponding to each component logistic
) corresponding to each component logistic 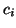 . A subset
. A subset
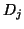 contains a point
contains a point 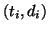 if
if
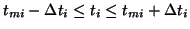 :
:
where 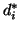 is the adjusted value of
is the adjusted value of 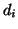 . The adjustment
is subtracting out the ``effects'' from other components,
leaving us with the (approximate) contribution of component
. The adjustment
is subtracting out the ``effects'' from other components,
leaving us with the (approximate) contribution of component 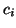 to this
data point. In other words,
In Figure 5C, the hypothetical data set plotted in Figure
5A is decomposed into subsets
to this
data point. In other words,
In Figure 5C, the hypothetical data set plotted in Figure
5A is decomposed into subsets 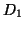 (circles) and
(circles) and
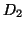 (crosses); similarly, the fitted curve is also decomposed into
its component logistics. Note that the subsets
(crosses); similarly, the fitted curve is also decomposed into
its component logistics. Note that the subsets 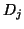 are not
necessarily mutually exclusive in the
are not
necessarily mutually exclusive in the 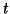 domain; in this example,
domain; in this example,
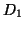 and
and 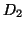 share points with common
share points with common 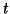 -values around
-values around 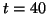 .
At these times, we can see that there are two concurrent growth
processes; in addition, we can also quantify how much of the growth
can be attributed to each process.
.
At these times, we can see that there are two concurrent growth
processes; in addition, we can also quantify how much of the growth
can be attributed to each process.
As we saw in Figure 3, we can apply the Fisher-Pry
transform to each component and its corresponding data subset. This
is useful because it normalizes each component on a semi-logarithmic
scale, allowing for easy comparison when plotted on the same graph.
Moreover, it allows the fitting of logistics using linear least
squares. The Fisher-Pry transform of components 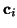 is
is
where plotting 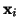 vs.
vs.
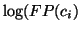 produces
a straight line. The component data subsets
produces
a straight line. The component data subsets 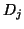 are transformed in
a similar manner:
Figure 5D shows the
Fisher-Pry decomposition of the hypothetical data.
are transformed in
a similar manner:
Figure 5D shows the
Fisher-Pry decomposition of the hypothetical data.




Next: Growth rates and the
Up: The Mathematics of Loglet
Previous: Definitions and notation
Contents
Jason Yung
2004-01-28
![]() logistic components
logistic components
![]() ,
where
,
where
![]() gives us a criterion for
decomposing the associated data set
gives us a criterion for
decomposing the associated data set ![]() into subsets
into subsets ![]() (
(
![]() ) corresponding to each component logistic
) corresponding to each component logistic ![]() . A subset
. A subset
![]() contains a point
contains a point ![]() if
if
![]() :
:
![$\displaystyle d^\ast_i = d_i - \sum_{j \neq i} \frac{\bold P_{j2}}{1 +
\text{exp} \left[ {-\frac{\ln(81)}{\bold P_{j1}}}(t - \bold P_{j3}) \right] }
$](img67.png)
![]() is
is