Generalization of the Bi-logistic model

Now we generalize the bi-logistic model to a multi-logistic model, where growth is the sum of 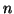$n$ simple logistics:

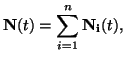$$\bold{N}(t) = \sum_{i=1}^{n} \bold {N_i}(t),$$ (6)

where

$$\bold{N_i}(t) = \frac{\kappa_i}{1 + \text{exp} \left[ {-\frac{\ln(81)}{\Delta t_i}}(t -t_{mi}) \right] }.$$ (7)

Figure 4 shows a Loglet analysis of a hypothetical data set fitted with the sum of five component logistics (shown in the box in the upper right hand corner). Here again, apparently complex behavior reduces to the sum of logistic wavelets. Note that ``growth'' processes also include processes of decline; in our model, this occurs when 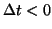$\Delta t < 0$ and $\kappa < 0$.

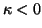Figure 4: A loglet analysis of a data set with five component logistics.