This paper is was published by the journal Technological Forecasting and Social Change in 2002.
Citation: Technological Forecasting and Social Change 69(3):243-262, 2002.

PDF file: DRAMTFSC.pdf

You can also download the data used in this publication: [ Microsoft Excel spread sheet ] or [ HTML table ]

DRAMs as Model Organisms for Study of Technological Evolution

NADEJDA M. VICTOR and JESSE H. AUSUBEL

ABSTRACT

The short, well-documented market life of generations of Dynamic Random Access Memory  (DRAM) computer chips makes them an excellent “model organism,” like the fruit fly, for study of  evolution, in this case technological.  Using classic models of logistic growth, substitution, and learning, we examine the global dynamics of eight generations of DRAMs  and forecast the market characteristics of the next DRAM generations.

1. Introduction

Biologists overcome problems of studying evolution by working with fruit flies and other short-lived animals and plants. The fruit fly Drosophila melanogaster is born, matures, and dies in a few weeks.  In front of an individual biologist's eyes, fruit flies are tested by the environment and the fit ones reproduce, passing on their tested inheritance through many cycles.

A student of the evolution of technologies, in contrast, generally lacks documented subjects that present several cycles.  During a lifetime, a technology researcher will see few cycles of technology from birth through testing to birth of successors.  If we define a generation of technology as a cohort with a common attribute, the technology researcher will see few generations rise and decline. Steel-making technologies, for example, required more than 50 years for 3 generations [1].  Industries such as autos, pharmaceuticals, and electric power measure the time of many of their products and processes in decades.  Thus, most technology researchers will see few consequences of birth and selection during the span of their patience and even careers.  Moreover, during slow technological evolution, recording of history may become imprecise.  Measurements may be neglected, and measuring devices themselves change.

Happily, the semiconductor industry has given birth to a fruit fly, a model organism for study of technological evolution.  Dynamic Random Access Memory (DRAM) chips cycle quickly from birth through testing by the market to new invention.  A generation of, say, 128 M DRAM dominates the market only a few years.  Because generations persist only briefly, their well-documented history now extends over 8 generations, making precise tests of classic hypotheses of technological evolution possible.  In this paper, we examine the fruit flies of technological evolution, DRAMs.

First, we introduce DRAMs and the attributes that identify generations.  We introduce the companies that give birth to them, products where their attributes are shown, and markets that test their fitness.  The rapid selection and passage of DRAM generations epitomize logistic substitution of one generation for another, an evolution by replacement, as well as test "Moore's Law."  The data quantify learning both within a generation and in the jump from one generation to the next, by mutation, one might say.  Despite the seeming chaos of competition, the extraordinary regularity of the passage of DRAM generations also permits forecasts of their future.

2. DRAMs

DRAMs are the highest-volume commodity semiconductors built today, with about 11 percent of the total semiconductor market [2], [3], [4].  “Dynamic" indicates that, for remembering the data, the memory chip requires every bit to be refreshed within a certain time period.  "Random Access" indicates that each cell in the memory chip can be read or written in any order.  The bits of a DRAM are arranged in cells (different memory locations) where each cell contains a specific number of bits.  For example, a 16 megabit (Mbit) chip, configured as 4M x 4Bit, means that there are 4M (4,194,304) cells with 4 bits each.[2]  The packing of these cells is the defining attribute of a generation and a standard measure of technological evolution.[3]

About 60 percent of all DRAM chips have typically been used in the PC industry. More than 50 percent of all DRAMs go to original equipment manufacturers such as Apple, Compaq, Dell, HP, and IBM.  The next largest market is the workstation/server market with companies such as HP, IBM, and Sun.  Most of the PC and workstation markets use memory modules, buying or subcontracting them from companies such as Kingston, Smart, and Viking.  Top semiconductor DRAM suppliers have included Hyundai, Micron, Samsung, NEC, Fujitsu, Mitsubishi, Hitachi, Toshiba, and IBM Microelectronics.  Fueled by the PC boom and the growing need for memory in all information appliances, the DRAM sector became the lead product in the overall integrated circuit (IC) market about 1990.

Three interacting forces form the environment that tests the fitness of DRAMs and thus evolution by replacement of generations.  The forces interacting and testing DRAMs are demand, supply, and technological change.  As implied, demand for DRAMs has linked closely with PC and memory upgrade sales.  As prices decline for DRAM, equipment manufacturers have increased the amount of memory they ship per computer.  Currently, the processes that most manufacturers use let them produce the 64M and 128M DRAM densities cost effectively, and during 2001 the 256M chip should also be cost-effective.  Technology constantly drives increasing density and smaller die size, and thus lower cost-per-bit memories.  To benefit fully from the higher speed processors, the market shifts to the new families of faster DRAMs. 

System requirements determine the technological changes as well as the need for DRAM evolution and, eventually, the specific solutions used.  For example, memory is no longer a “one-size-fits-all” product.  The "page mode" memories have moved towards "extended data out," or EDO, and memories will soon move to synchronous DRAM, which will increase performance by up to four times that of today's memory products. 

As the DRAM market changes with new architectures and higher-performance devices, the balance of supply and demand adjusts with tighter supply of the new architectures and more pricing pressure on the older products.  DRAM manufacturers try to increase their revenues, and their managers do what they can to keep the costs down. Many DRAM companies have quit the business, been sold, or merged with other companies.  Companies have reeled from huge drops in chip prices, as well as from economic fluctuations, e.g., in the Asian countries.  In this environment, they cut capital spending and capacity expansion, and seek to focus on core competencies.  Designing next-generation process technology has become so expensive that DRAM companies now commonly work together.  What is startling, as we shall see, is that this extremely competitive, turbulent environment for firms has produced very smooth, regular evolution and predictable outcomes at the level of the industry.

3. Price and volume history

Prices signal the attributes of products and the balance of environment and invention.  Annual average prices for each of eight DRAM generations in US$ per Mbit  declined sharply in most years since the product record begins in 1974, as evident from Figure 1.[4]  4K chips had the lowest rate of average annual price reduction, less than 15% yearly.  The 64k chips marketed 1994-1998 had the highest rate, 62%.  In some years price reductions slowed, and sometimes DRAM prices even rose.  Fastest reductions generally happened during the first 2-3 years the new DRAMs are in the market. The price falls through the next couple of years, then stabilizes as soon as the successor generation of chips is available, and even grows slightly in the twilight of the product’s lifetime.

The early price declines reflect economies of scale and increasing competition, as well as a learning curve for manufacturers, an aspect we shall discuss in detail later. The final price increases suggest decreasing economies of scale, declining competition as fewer manufacturers supply the particular chips, and captive markets. The price rises may also illustrate “forgetting if not doing” or a “forgetting curve” symmetrical to “learning by doing” and the learning curve.

Other “artificial” or non-market factors may affect prices.  As the result of the U.S.-Japan Semiconductor Trade Agreement in late 1986, the prices of all DRAM generations declined more slowly in 1987 and even grew in 1988.  The Agreement came from US insistence that Japan limit its export of semiconductors (mainly DRAMs) to America to help some segments of the US semiconductor industry.[5]  Small imbalances in supply tend to affect price greatly, and the DRAM market seems to go through business cycles of four to five years.  Nevertheless, the similarity of the shapes of the individual curves in Figure 1 and the steady diagonal they collectively form suggest the immense power of the underlying market dynamic.

Price can be measured not only directly against time, but also against output, for example, annual global shipments in Mbit.  As evident in Figure 2, this relationship again reveals extremely regular individual and collective behavior.   Collectively, the downward diagonal movement from left to right shows that, while shipments have increased by a factor of 10^5th, the DRAM price has dropped by a factor of 10^6th, in steady proportion.  The total DRAM sale in Mbit in 1998 was more than 4 million times 1974, an increase of about 90 percent annually.

Individually, the trajectory of each DRAM generation has moved clockwise through changes in annual revenue and prices, again in stable ratios.  The result is that, in spite of falling prices for every DRAM generation, the total revenue from the sales of each generation increases. The 4M generation achieved the peak annual revenue so far with $21 billion in 1995.

The shipments and prices, of course, form industry revenue (inset of Figure 2). DRAM sales increased dramatically, with average annual revenue growth rate about 22 percent in 1974-1998.   The most lucrative year was 1995 with total revenue about $40 billion or more than 30 % of the IC market, compared to $6.4 billion or 15 % of the market 5 years before.  After 1995 DRAM sales decreased and reached only about $14 billion in 1998, even as the number of parts and bits shipped continue to grow.  The cause may be a 4-5 year market cycle, with 1996-1998 a low point where capital spending did not keep up with increasing demand.  Alternately, it may reflect a more fundamental change, such as the replacement of DRAMs by different memory technologies.[6]

Omitting prices, we can also assess shipments against time.  Counting simply the millions of units shipped suggests a sporadic market evolution (Figure 3).  Total units multiplied by 4 times from the 16k to the 64k DRAM, then remained flat for 256k and 1M, before doubling again for the 4M chip.  However, counting the sales in Mbits shipped reveals a different and more consistent story (Figure 4).   This measure shows beautifully regular market growth: each improved DRAM matches a significantly larger market, which can be satisfied by better as well as more chips.

4. Logistic substitution in DRAM generations

The swift rise of populations of fruit flies in a jar became the classic (1925) subject for Raymond Pearl [7] to depict with the logistic curve, which rises in a sigmoid at first exponentially as the flies multiply but then levels as they exhaust the food in a jar.  The swift passing of the generations of DRAMs in Figure 4 invites depiction by the same logistic curve [8], [9].  Later we shall see how learning permits DRAMs to mimic the exponential multiplication of flies.  For now, however, let us extend the logistic curve from the simple rise of a single generation distinguished by an attribute like 128 M to its rise fall and thus evolution.  The rising hills of Figure 4 affirm Montroll’s [10] observation that evolution may be usefully defined as a series of replacements.

In technological evolution, incremental improvements in a device meet demand for better performance until some tough limit in a device appears and motivates the search for a superior alternative that conforms to the new requirements and opportunities.  On the one hand, a device grows logistically to a limit of performance and then is replaced by another whose performance also grows logistically.  At the same time, the device or product penetrates the markets logistically, and then is itself replaced by the logistic market penetration of its successor.  We now explore logistic growth as a framework for description of the replacement of DRAM generations.

Using the measure of cumulative sales in units shipped, we see first that the successive DRAM generations do match the logistic paradigm, beginning with exponential growth and then slowing symmetrically as their limits are approached and the “S-shape” achieved (Figure 5).[7]  Our next check is based on Fisher and Pry [11], who described the evolution of the fractional market share and not the total production of the particular commodity.[8]   The Fisher-Pry transform of the DRAM cumulative sales shows superb regularity, as idealized curves for each DRAM generation running exactly parallel to each other at similar distance indicate.[9]

To check quantitatively how close to ideal the DRAM system behaves, we use the Loglet Lab software to estimate the saturation, midpoint, and growth time parameters (Table 1).[10]   The growth time, the time required for the product to go from 10% to 90% of its expected extent, varies only between 3.9 and 6.3 years, and the midpoints are always three or four years apart.  While these two measures of DRAMs show Prussian order, the saturation levels are less orderly.   Although the saturation level of cumulative sales for each DRAM generation exceeds the prior, ideally we would find a constant positive ratio of saturation levels.  The ratios range from 1.1 to 4.2, although the last three have been about 1.5.

Logically, DRAM demand cannot be unlimited in the long-term, i.e., the saturation levels should have their own saturation.  In such case, we might expect that saturation levels for DRAM cumulative sales at the outset grow rapidly with fluctuations as they “find” their trajectory, then climb smoothly in an exponential phase, later slow, and finally decline when a radically new memory technology appears on the scene.  When we examine total cumulative DRAM shipments, we as yet find no sign of saturation (Figure 7).  Rather, a regression analysis confirms with an R² of 0.99 an exponential relationship with the total DRAM demand in Mbit doubling every 14 months during the last 24 years.[11]  

In 1965 Gordon Moore, co-founder of Intel, observed that the number of transistors per square inch on integrated circuits had doubled every year since the circuit’s invention.  Moore predicted that the trend would continue for the foreseeable future.  Subsequently, the pace slowed a bit, but data density has doubled about every 18 months, and this rate popularly defines “Moore's Law,” which Moore himself has blessed.[12]

With the fruit flies of DRAM, we can test Moore’s Law exactly.  We test it by relating DRAM density to the first year a DRAM generation reaches the market  (small right-hand “window” of Figure 7).   Regression analysis confirms that IC densities increase exponentially to the present, as every three years a new DRAM generation with 4 times the storage capacity as the last appears on the market, matching Moore’s Law of power doubling every 18 months.  Unsurprisingly, comparing the time between midpoints of adjacent generations gives the same 3 years, because the midpoint of the logistic is related to the arrival of the next DRAM generation on the market.

Many experts, including Moore, expect Moore's Law to hold for at least another two decades [14].  We find no evidence of slowing but remain agnostic on how long the exponential phase will continue.   The question of the logical limit to humanity's demand for memory is quite open.  Certainly communication and information processing can be many orders of magnitude higher than today even in Silicon Valley, and most of the world today has only a tiny fraction of the Valley's chips.

To what extent do the regularities of DRAM market development allow projections?  To answer this question we first analyze technological learning in DRAM generations.

5. Learning in DRAM generations

Goods and services may rise and decline in the market because manufacturers and service providers learn.  A classic concept in the analysis of technological evolution is the experience curve or effect of learning-by-doing [15], [16], [17].  This concept affirms that at the center of technological change is technological learning: the more experience is gained with a particular technology, the larger are the improvements in performance, costs, and other important characteristics.   Aircraft builder T.P. Wright [18] defined “learning-by-doing” in 1936 as a relatively permanent change in behavioral tendency that occurs as result of reinforced practice. Empirical studies of the production process in various industries have demonstrated a positive association between current labor productivity and measures of past activity like past cumulative output or investment.

The conventional form of the learning curve is a power function:

Y=a X^b                                               (5)

where Y is the cost of the technology; b is the progress ratio; X is the cumulative installation of the technology; and a is a scale coefficient that reflects the cost of the first installed item.[13] 

Because production and cost data for different DRAM generations are unavailable on the global level, we examine cumulative shipments in million units and in Mbit versus DRAM price (Figure 8).  For each DRAM generation, we see the pattern of learning, that is, descending price, often with a knee late in its lifetime.  Equally important, the replacement of one DRAM generation by another can be viewed as the transition from one learning curve to another, in most cases decisively cheaper, one.  While strictly speaking each DRAM generation so far has been 4 times more capable than the prior, Figure 8 suggests that measured by price performance ($/Mbit) the difference between generations is more irregular but averages out to about a factor of 5.   Surprisingly, the learning within a generation measured by price performance usually approaches 100!  The ratio confirms that a firm cannot survive by innovation alone.   It also suggests that other product attributes, such as miniaturization, count strongly in the marketplace.

Aggregating all the curves into a single curve, as the inset of Figure 8 practically does, illustrates the general trajectory of DRAMs’ learning-by-doing: lower prices and higher volume of sales.  Highly significant regressions show that learning rates of shipments in Mbits versus price vary from 16 percent to 35 percent across generations with an average about 28 percent (Table 2).  Slower rates for the recent 16M and 64M generations suggest a tendency toward decreasing learning rates.

Other analysts have examined learning-by-doing in DRAM production.  Baldwin and Krugman [19] estimated 28 % learning rates for 16K DRAM production in contrast to our 24%.  Irwin and Klenow [20] reported learning rates that varied from 16% to 24 % across generations that we estimate at 24% to 33%.  The results may differ because we used the latest data currently available at the global level and additional generations.  Also we used average annual rather than quarterly data, and cumulative annual shipments in Mbit rather than in millions of units.

6.DRAM market forecasts

Accurate predictions are the best proof that models work, and so we venture some forecasts of the DRAM market based on the logistic substitution model and learning curve equations. We assume the following, based on our empirical findings:

• Moore's Law continues to hold, so the capacity of DRAMs doubles every 18 months.
• The DRAM market increases exponentially, with the total DRAM demand in Mbit doubling every 14 months.
• Learning rates tend to decrease with new DRAM generations.
• Total revenue from sale of every new DRAM generation exceeds the total revenue from sales of the prior generation.
• Annual revenue from sales of DRAM generations increases irregularly, going every 4-5 years through a cycle related to the growth time of the generation that dominates. The growth time coefficients vary slightly from generation to generation, with the average growth time 5 years.

Table 3 introduces our estimates of the historic parameters 1974-1998 and forecasts for 2001-2005.  Parameters for the historical trends were estimated using the Loglet Lab software.  In the absence of data for the imminent 128M and 256M generations,[14] saturation levels of cumulative shipments for 128M and 256M generations are estimated by simple regression established on the relationship between saturation levels and DRAM IC densities.

The forecasts through 2005 of 10 DRAM generations with the results converted from cumulative Mbit into annual million units (Figures 9 & 10), emphasize the narrow and perhaps abortive window of 128M DRAMs. The growth time for 128M was estimated as 2.5 years instead of 4-5 years, as in previous generations.  The reason is that 256M is expected to appear in the market soon after 128M, and these two generations will be compete closely.[15]  The memory market will likely shift fast to 256M DRAM, driven by demand for high-capacity memory to power computing systems for e-commerce and the Internet.

The learning curve equation and a learning rate of 22 % make possible estimates of the price dynamics for 1999-2005 (Figures 11 and 12).  In our forecast the chip price trends for 128M and 256M are moving toward the so-called "bit cross" phenomenon, in which the price of the 128M DRAM falls below the combined price of two 64M DRAM, and the price of the 256M DRAM falls below a combined price of two 128M DRAM.  Thus, consumers will move from 128M to 256M much faster than, for instance, from 16M to 64M.  The forecasts of prices and shipments in turn determine the annual revenue from sale of all DRAM generations (Figure 13).  Notably, we estimate the revenue from DRAM sales will attain the level of 1995 only in 2004 and than will fall again according to the cycle.  

Investments in new DRAM generations depend on fluctuating revenues from sales of previous generations.   Appearance of the 128M generation on the market could mean that accumulating the resources for R&D is becoming harder, as the transfer of production lines to 128M DRAM requires less additional facility investment than the previous generation shift from 16M to 64M.  If so, the next generation after 256M could be 512M.   A 512M DRAM generation could signal the end or downward adjustment of Moore’s Law, as doubling IC density would then require 24-30 months.[16]  Still, the generation growth time could stay about the same or even slightly decrease.  Thus, revenue cycles will shorten and, with price stabilization, the revenue curve will smooth.

Our projection of DRAMs raises the fundamental issue of the relationship between the logistic equation and the learning equation.  The DRAM data offer the chance to test several hypotheses about logistics and learning.  Here we merely stress the potential of this model organism for such testing.  The combination of “logistic” behavior based on cumulative installation of the technology as the dependent variable and “learning curves” based on cumulative installation of the technology as the independent variable should successfully simulate technological substitution.  If the market includes only one technology (no competitors) and the technology is improving, cumulative installation may increase exponentially.  If technologies are competing, the installation of the technologies depends (among other things) on the cost of installation.  A particular technology will tend to increase its installation with decreasing cost (learning), become dominant, and reach the maximum.  When the cost of a new technology roughly matches the cost of a dominant technology, the technology leader will lose market share and eventually dominance.  The combination of the logistic and learning equations for n different technologies from the same innovation “family” (such as DRAMs) and the fact that the dynamic of the “family” itself has a logistic nature can be used for long-term forecasts of technological evolution.  Time will test our own projection.

7. Conclusions

The rapid rise and decline of the electronic fruit flies, DRAMs, before our eyes provides precise numbers to test classical models of technological evolution.  The unusual features of DRAMs are exceptionally well-documented technical and market performance and rapid cycle times that permit analysis across many generations.  Because DRAMs exemplify technology of the information era, they add importance to convenience for analysis.  They were integral to the emergence of the personal computer and prospered as machines needed more memory capacity.  Driven by availability of powerful new microprocessors and increased complexity of software operating systems and applications, the average memory per PC doubled between 1994 and 1996, and doubled again by 1998.  The demands of multimedia mean continued market growth for DRAMs.  Despite seeming rapid change and turbulence, our first conclusion is that these symbols of the new economy play by absolutely traditional rules.  Their record fits perfectly with classic models of logistic substitution and learning curves.

What do the conclusions imply for researchers, engineers, investors, and managers?  Prompted by the analysis of DRAMs, researchers will wonder whether the exponential rise of an early logistic curve and Moore’s Law applies to many technological “species.”  Unfortunately, the performance of most technologies is not quantitatively documented over several generations.  So, a worthwhile program would build the database in a range of industrial sectors to examine their equivalents of Moore's Law. Merely agreeing on and monitoring simple master measures of technical progress would be valuable (and challenging) in many sectors.  The applicability of such Laws and their parameters could benchmark progress for firms as well as industries.

For engineers, the DRAM analysis shows the feasibility, indeed urgency, of performance targets and timetables.  Aiming too low or too high, too early or too late, will assure market failure.  Investors and managers need to understand the same point, but they also recognize that political deals, such as international trade agreements, influence who wins.  We do not know how to model politics, but investors and managers may know how to manipulate it.  The smoothness of the DRAM curves shows that politics has little or no long-run effect on the evolution of the technology per se, but it may largely determine who makes money from it.  Investors and managers should also note the predictable tendency of R&D to cost more as scale grows and thus concentrate firms in an industry.

Managers should take note that, for all their famous entrepreneurial independence, the heroes of Silicon Valley and other high tech regions have collectively behaved like perfectly programmed robots.  Although the environment at the level of the individual manager or firm may appear extremely turbulent and unpredictable, outcomes at the level of the industry are absolutely fated.

In conclusion, we believe DRAMs merit a place, like the fruit fly, as a model organism for study of evolution, in this case technological.  We urge that data be made readily available about DRAMs so they can be studied in great detail in all their aspects, for development, comparison, and calibration of models, and for education of all those interested in principles of technological evolution.

Acknowledgements: We thank Arnulf Gruebler, David Hodges, Perrin Meyer, Nebojsa Nakicenovic, and Paul Waggoner for assistance.

References

1. Gruebler, A.: Technology and Global Change. Cambridge University, Cambridge UK, 1998.
2. Integrated Circuit Engineering Corporation, Status 2000, Scottsdale, AZ, 2000.
3. Garrett, B.: Four forces shape DRAM evolution, 2000, http://www.eetimes.com/story/OEG20000204S0015
4. Macher, J.T., Mowery, D.C., and Hodges, D.A.: Semiconductors, in U.S. Industry in 2000: Studies in Competitive Performance, Board on Science, Technology, and Economic Policy, National Research Council, National Academy, Washington DC, 245-286, 1999.
5. Johnson, B.T.: The U.S.-Japan Semiconductor Agreement: Keeping up the Managed Trade Agenda, Backgrounder No.805, January 24, 1991.

http://heritage.org/library/archives/backgrounder/bg805.html

6. Johnson, B.T.: Let the U.S.-Japan Semiconductor Agreement Expire, Backgrounder Update No. 277, May 30, 1996.

   http://heritage.org/library/categories/trade/bgup277.html

7. Pearl, R.: The Biology of Population Growth,  Knopf, New York , 1925.
8. Banks, R.B.: Growth and Diffusion Phenomena. Mathematical Framework and Applications. Springer, Berlin, 1994.
9. Meyer, P.S., Yung, J.W., and Ausubel, J.H.: A primer on logistic growth and substitution: The mathematics of the Loglet Lab software, Technological Forecasting and Social Change 61(3), 247-271 (1999).
10. Montroll, E.W. Social dynamics and the quantifying of social forces, Proceedings of the National Academy of Sciences USA 75(10), 4633-4637 (1978).
11. Fisher, J.C., and Pry, R.H.: A simple substitution model of technological change, Technological Forecasting and Social Change 3, 75-88 (1971).
12. Yung, J.W., Meyer, P.S., and Ausubel, J.H.: The Loglet Lab software: A tutorial, Technological Forecasting and Social Change 61(3), 273-295 (1999).
13. Moore, G.E.: An update on Moore’s Law, speech to Intel Developers Forum, September 30, 1997,San Francisco, http://www.intel.com/pressroom/archive/speeches/GEM93097.HTM
14. Moore, G.E.: The continuing silicon technology evolution inside the PC platform,   http://developer.intel.com/update/archive/issue2/feature.htm
15. Argote, L., and Epple, D.: Learning curves in manufacturing, Science, 247, 920-924 (1990).
16. Lamoreaux, N.R., Raff, D.M. and Temin, P. (eds.): Learning by Doing in Markets, Firms and Countries, National Bureau of Economic Research Conference Report, University of Chicago, Chicago (1999).
17. Neij, L.: Use of experience curves to analyze the prospects for diffusion and adaptation of renewable energy technology, Energy Policy, 23(13), 1099-1107 (1997).
18. Wright, T. P.: Factors affecting the cost of airplanes, Journal of Aeronautical Science, 3, 122-128, (1936).
19. Baldwin, R.E., and Krugman, P.: Market access and competition: A simulation study of 16K random access memories, in Empirical Methods for International Trade, Feenstra, R.C., ed., MIT, Cambridge MA, 171-197 (1988).
20. Irwin, D.A., and Klenow, P.J.: Learning-by-doing spillovers in the semiconductor industry, Journal of Political Economy 102(6), 1200-1227 (1994).

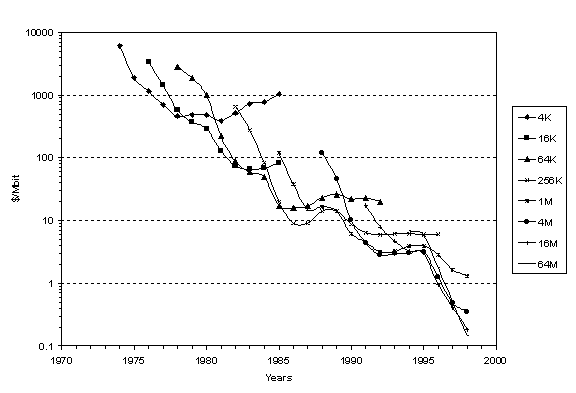Fig. 1. Annual average prices for DRAM generations. Sources of data: [2], [20]

.

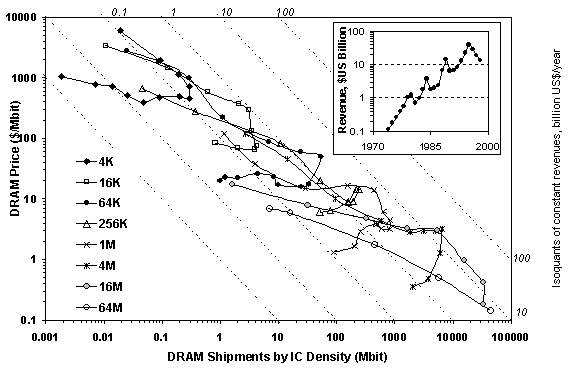
Fig 2. DRAM prices versus annual shipments by IC density in logarithmic scale. The dashed lines are isoquants of constant annual revenues in billion US$ per year. The inset window shows total annual revenue from DRAM sales in semi-logarithmic scale. Sources of data: [2], [18]

.

Fig. 3. DRAM shipments. Sources of data: [2], [20].

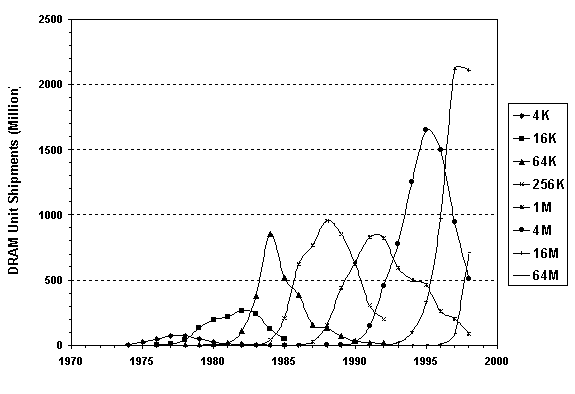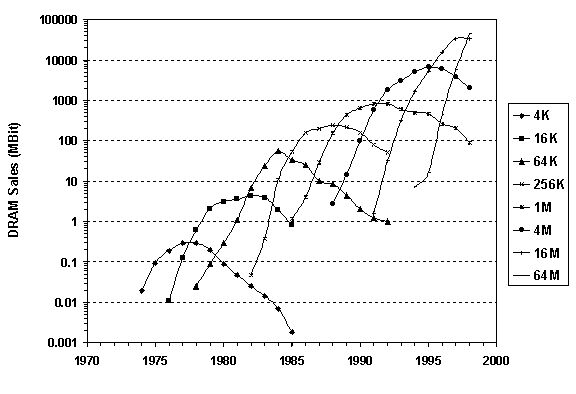
Fig. 4. DRAM sales in Mbit by IC density. Sources of data: [2], [20]

.

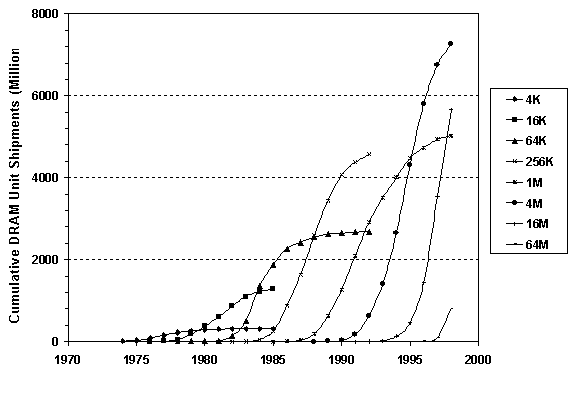
Fig. 5. Cumulative DRAM shipments. Sources of data: [2], [20].

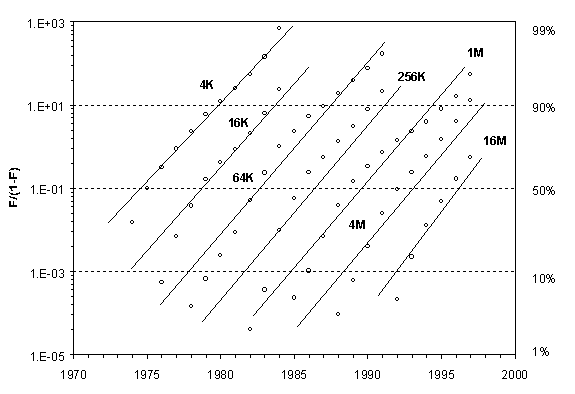
Fig. 6. Actual DRAM shipments (circles) and ideal trajectories (straight lines) in Fisher-Pry transform. Sources of data: [2], [20]

.

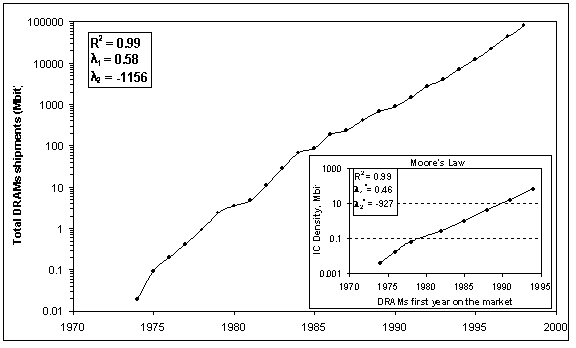
Fig. 7. Cumulative shipment of all DRAMs  and results of regression estimation. The inset window shows IC density versus first year of the DRAM generation on the market and the result of regression estimation. Sources of data: [2], [20]

.

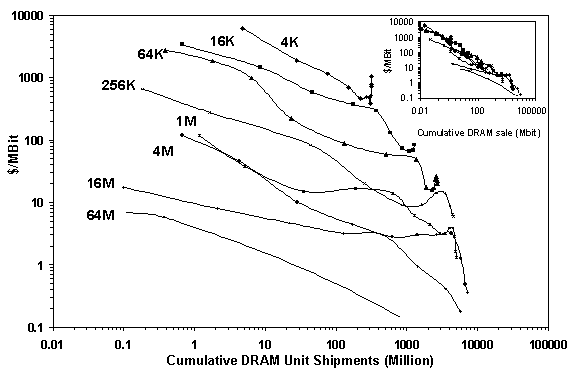
Fig.  8. DRAM prices versus cumulative DRAM shipments in units for eight DRAM generations. The inset window shows DRAM prices versus cumulative DRAM sales in Mbit.  Sources of data: [2], [20].

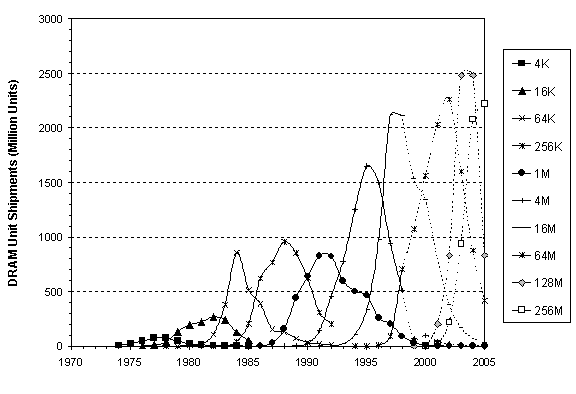Fig. 9. Historical and projected DRAM shipments. Sources of data: [2], [20]

.

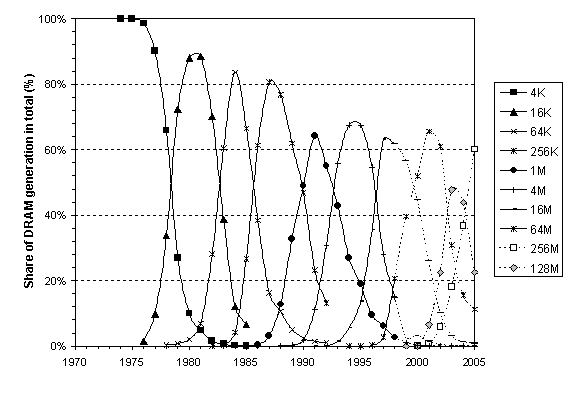
Fig. 10. Shipment of DRAM generations as shares of total shipment: historical and projected. Sources of data: [2], [20].

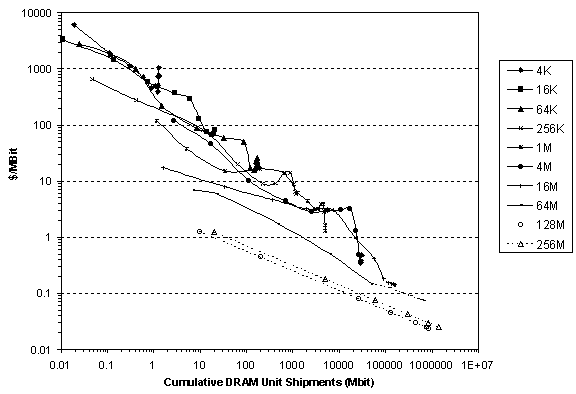
Fig. 11. DRAM prices versus cumulative DRAM shipments: historical and projected. Sources of data: [2], [20]

.

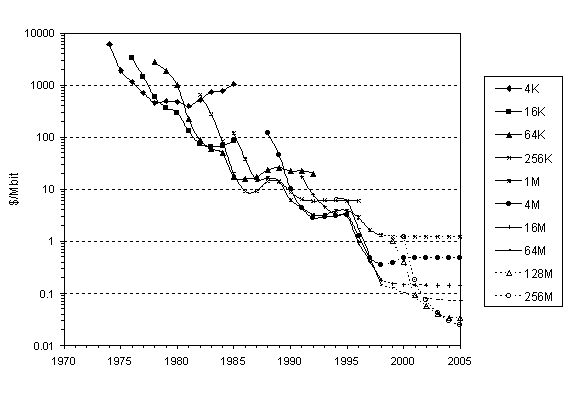
Fig. 12. Annual DRAM prices: historical and projected. Sources of data: [2], [20].

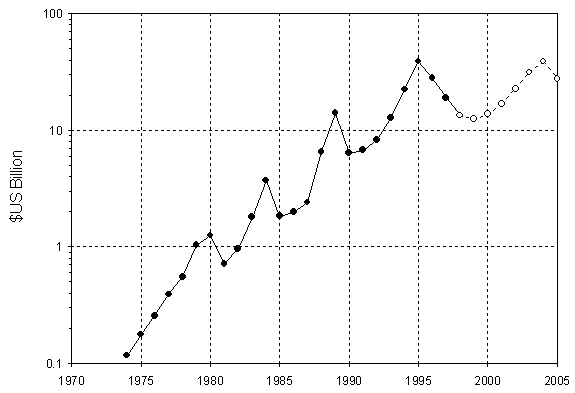
Fig. 13. Total annual revenue from DRAM sales: historical and projected.  Sources of data: [2], [20]

.

Table 1

Estimation of logistic curve parameters for DRAM generations

Notes:

* - K, or maximum value of this logistic and  ratio to prior saturation (in parentheses)

** - b,  or  the point of inflection of the curve

*** - Dt, or time in which the logistic goes from 10% to 90% of its expected saturation level

Table 2

Learning curve estimates for DRAM generations

Notes:

* -  Rate of price reduction as cumulative sale increases (with standard error)

** -   Price reduction per doubling of cumulative sale (measured in Mbit)

Table 3

Historical and projected estimates of logistic curve parameters for DRAM generations

Notes:

* - K, or maximum value of this logistic

** - b,  or  the point of inflection of the curve

*** - Dt, or time in which the logistic goes from 10% to 90% of its expected saturation level.

URL: http://phe.rockefeller.edu/LogletLab/DRAM/