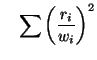 is minimized
is minimized
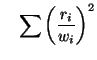 is minimized
is minimized
With historical time-series data, a more accurate analysis may be
achieved by focusing on ``quiet'' periods and excluding unrepresentative
data; for example, an analysis of nuclear testing data might be
improved by excluding data from the years around the signing of the
Nuclear Test Ban Treaty. Exclusion is accomplished by setting
![]() for certain values of
for certain values of ![]() . This is sometimes referred to as
``masking'' data, as we are hiding some of the points from the
fitting engine.
. This is sometimes referred to as
``masking'' data, as we are hiding some of the points from the
fitting engine.
Loglet Lab accommodates masking of the data. However, it does not allow use of user-specified weight vectors, though this functionality could be added in the future.